 accesses since December 22, 1997
accesses since December 22, 1997 copyright notice
copyright notice
 link to published version: Communications of the ACM, March, 1998
link to published version: Communications of the ACM, March, 1998
 accesses since December 22, 1997
accesses since December 22, 1997Normally, my columns are a product of accretion. This one, however, was interrupt driven. The trigger in this case was the convergence of two independent events: my response to Peter Wegner's article "Why Interaction is More Powerful than Algorithms" which appeared in the September, 1997 issue of CACM and the appearance of a new book by ACM Press, Capers Jones, "The Year 2000 Software Problem: Quantifying the Costs of Assessing the Consequences." Not one to ignore kismet, this manuscript was born.
The story unfolds this way. Following the publication of his article, Peter Wegner and I were discussing various computational metaphors for interactive computing. I found Wegner's argument that algorithmic computing is weaker than interactive computing compelling. In addition to his formal arguments showing that interaction machines cannot be expressed by Turing machines and his incompleteness proof that interactive systems cannot be expressed by first-order logic, there are several practical examples showing that interactive services like banking or airline reservation cannot inherently be realized by non-interactive (Turing machine) systems.
I suggested that there were likely examples which went beyond the inadequacy of algorithmic computing in handling the interactivity. One that came to mind was the "Year 2000 Problem" (a.k.a., "millennium problem," "millennium bug"). I suggested that what really underlay this problem was that computer users (both physical and digital) take each system report of a correct date as a confirming instance of the hypothesis that the system's reported date is always correct. What the year 2000 problem shows is that correct time observations were not confirming instances of this hypothesis at all, but rather one where "date" terms were unknowingly temporally qualified. That is, we take a system date reports to be "this is the current date," when in fact the report should have been interpreted "this is the current date only if the current date is prior to year 2000." Most experimental computing is predicated on the fact that successful runs confirm correctness, and I was trying to show that the Year 2000 problem provided a counterexample. My promised elaboration was triggered by the appearance of Capers Jones book.
What's the true storage cost of two bytes? Minuscule in the individual case, wasteful excess which multiplied by the billions. The year 2000 problem is about a couple of bytes: a couple of bytes of storage saved in databases, a couple of bytes saved in silicon, a couple of bytes saved in BIOS routines, a couple of bytes spared by operating system function calls, a couple of bytes of I/O. This problem is about a couple of bytes.
The result of the computing community's byte-parsimony is a multitude of computing systems which will not, in the normal course of things, roll-over to year 2000 at the end of this century. Many systems will roll back to 1900 instead. Others might pass beyond the millennium threshold correctly, only to fail to roll over from 2099 to 2100. Still others may fail to advance beyond a pre-determined elapsed time in seconds since a certain starting date. These anomalies are motivating organizations worldwide to prematurely retire their computer systems, scramble for patches and work-arounds, and establish year-2000 rapid response teams to deal with all of the glitches which the other techniques fail to address. The aggregate worldwide cost of dealing with this problem is staggering - by some estimates in the hundreds of billions of dollars, but more on that later. How did we come to this?
Flashback to the 18th century Scottish philosopher, David Hume. - Ok, this is going to be a bit of a stretch, but bear with me. In a few pages we will converge on a point of enlightenment, or at least raise the Year 2000 Problem to a lofty theoretical level it may or may not deserve.
Hume was skeptical about finding a foundation for inductive reasoning - the inference from particular to general. We can't come to "know" that the sun will rise daily in the same way as we "know" the equality of 2+2 and 4, he argued, because reason is not the source of inductive beliefs: induction is neither rational or logical. How, Hume wondered, could one justify induction. Clearly it was beyond the capacity of deductive reasoning. But an inductive justification would be viciously circular. Thus, he concluded that inductive reasoning can't be justifiable in the customary (i.e., deductive) sense of the term at all - we have, as it were, an inductive paradox which, for convenience, we'll call the "old riddle of induction." Inductive reasoning works, Hume thought, not because it involves the justified inference from the particular to the general, but because the cause-effect relations and associations involved are internalized in some sort of "instinct." The legitimate expectations on which our behavior is based - that the sun will rise in the East tomorrow at about the same time as today, that the trade winds will continue to blow, that the seasons will change - are all expectations founded on this human instinct.
What does Hume have to do with the Year 2000 problem, I hear you ask. Be patient and read on.
So, Hume leaves us not only with his "old riddle of induction", but also with an escape clause: we can account for our faith in inductive reasoning by appeal to basic instinct. Induction isn't rational, but it works so well as a foundation of our beliefs that we needn't worry much. The "old riddle of induction" dissolves away.
Is that the end of the matter? In a word, no. A paradox remains which will tie in to the Year 2000 problem.
Flash forward to the mid-1900's when a Harvard philosopher, Nelson Goodman, investigates Hume's work and concludes that Hume has conceded too much to his critics. The "vicious circle" isn't really vicious at all. Goodman claims that inductive reasoning, just like deductive reasoning, is justified by conformity to appropriate, general rules. If, for example, we predict tides which don't arrive, we adjust the rules that gave rise to the prediction. So it is with deduction. If the axiom of specification produces a contradiction (ala Russell's Paradox), we substitute another less problematic axiom, or introduce a set theory based on types, or whatever else is necessary to fix the problem. Induction should fare no worse than deduction in terms of its justification.
However, just as the "old riddle" is solved (or dissolved), Goodman finds a "new riddle." The new riddle has to do with hypothesis testing.
In inductive reasoning, hypotheses are both generalizations of, and predictors of, evidence statements. As Goodman observes, the fact that one copper wire conducts electricity is confirming of the hypothesis that copper conducts electricity, but the fact that one student in class is a third son does not confirm the generalization that all students in the class are third sons. Generalizations from evidence statements are only possible when the hypotheses are "law-like.
Suppose, Goodman suggests, that we observe that all emeralds before some time, t, are green. Each observation of a green emerald prior to t is therefore a confirming instance of the hypothesis that all emeralds are green. Next, let's introduce another predicate, "are grue", such that an object is grue just in case it is green before t, or blue thereafter. The same observations now support the claim that all emeralds are grue. Both predictions are equally supported, but those involving "grue" is not supported to the same degree. The reason is that it the instances of grue-ness betray a linguistic coincidence, rather than a law-like regularity. The "new riddle" of inductive reasoning (a.k.a., Goodman's Paradox) derives from the fact that we cannot always distinguish law-like regularities from contingent or accidental ones. We have no straightforward way to distinguish between the case where light bending around the moon during a solar eclipse confirms Einstein's General Theory of Relativity on the one hand, than Aries' presence in the house of Mars with solar exaltation confirms a cookie's fortune.
You've stuck it out this far. It's downhill from now on.
The genesis of the year 2000 problem is seen to be an instance of the "new riddle of induction." It results from the mistaken belief that a computer date stamp is projectable - that is confirming of a hypothesis. We blithely assumed that an operating system date stamp satisfied the predicate "___ is the current date on the Gregorian calendar" when, in fact, the predicate was "___ is the current date on the Gregorian calendar only before time, t; and not thereafter." The accuracy was contingent and not law like.
Actually, the problem is even worse than that. Sometimes it's there are several layers of non-projectable predicates involved. I'll use DOS to illustrate the point. We take the result of function 2Ah of interrupt 21h ("Get Date") to be a confirming instance of the hypothesis that this function produces the current date in register CX. Such is not the case. Unbeknownst to us, DOS only recognizes the contents of CX if it falls within the range 1980-2099 (2099 is time t in this case). But the reason for this constraint betrays even more convoluted logic beneath DOS. DOS function 2Ah retrieves date information from the ROM BIOS services. However, subservice 04h of BIOS interrupt 15h ("Get Real-Time Clock Date") actually only returns the century (either 19 or 20) in register CH and the half-word integer equivalent of a two-digit year in CL. So the 4-digit integer date that the DOS function reports is already the product of interpretation by the OS. But it doesn't stop there. The DOS FILE_DATE values, offset 18h from in the directory entry, is even a more corrupted version of a date stamp. In this case, the reported date is a compression of the DOS reported date according to the formula ((year-1980)x512)+(monthx32)+day. Hence, December 31, 1999 becomes the unsigned word integer 279Fh (10,143). It is interesting to note that the roll-over for the file date would actually be 1980+2**7 years=2108, but since DOS will only recognize the 20th and 21st centuries, the file date will be undefined under DOS beyond 2099. The point is that none of the associated predicates of these functions and interrupts are projectable beyond some time, t, in the near future. The new riddle of induction rears it's ugly head in countless ways. The "new riddle" of induction is to be found in the very bowels of our BIOS.
These sorts of problems exist in all complex interactive environments. Some, like those above, may be a result of incorrect software interpretations of hardware. Most, however, will be a result of semantic confusions engendered within software systems such as non-monotonic code expansion and confusing extensional and intensional meanings of variables.
The root cause of our present malady is byte-conservation. The lengths to which we have gone to save a few bytes would do justice to endangered species. But we may not have accomplished much in the end. Capers Jones quotes Leon Kappelman who has calculated that the cost to fix the Year 2000 problem will eat up all of the savings we have accumulated by compressing dates in the first place. Jones adds, "The Year 2000 problem actually originated as an explicit requirement by clients of custom software applications and the executives responsible for data centers as a proved and seemingly effective way of saving money. Many programmers knew that the clock would run out ..."
So what are the estimated costs. Capers Jones offers a wealth of information on this subject. Consider his prediction of US repair costs for the Year 2000 in Table 1, below.
| INDUSTRY | EFFORT | COSTS |
|---|---|---|
| (In person months) | (In $billions) | |
| military | 1,909,091 | $14.3 | finance | 450,000 | 4.9 | manufacturing | 555,556 | 4.7 | communications | 423,529 | 4.2 | services | 555,556 | 4.4 | insurance | 450,000 | 4.1 | wholesale | 517,647 | 3.9 | federal | 400,000 | 3.2 | defense | 266,667 | 2.9 | retail | 412,500 | 3.1 | software | 193,421 | 1.7 | municipal | 150,000 | 1.1 | health care | 111,563 | .89 | states | 100,000 | .77 | energy | 87,500 | .70 | transportation | 82,031 | .66 | other | 1,800,000 | 15.1 | TOTALS: | 8,465,060 | $70,753,562,795 |
(Adapted from Capers Jones, The Year 2000 Software Problem, ACM Press, 1997. Used with permission.)
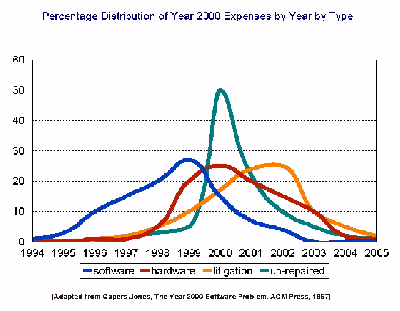
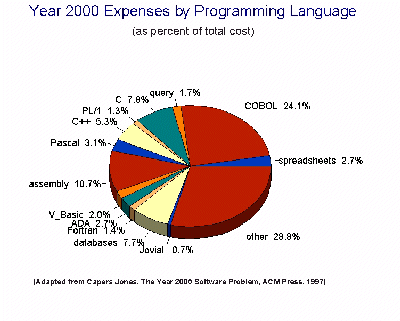
Jones predicts a $70 billion dollar loss in the U.S. alone for Year 2000-related software problems. What is more, this ignores the costs of repairing databases and data warehouses which he hypothesizes could reach another $125 billion. Figure 1 shows how these expenses will break out by year by type. As can be seen, the litigation costs of the Year 2000 problem only begin to express themselves. Figure 2 shows how these expenses break out by programming language as a percentage of the $70 billion dollar costs.
|
|
We illustrated the Year 2000 problem by means of a general problem with inductive reasoning called the "new riddle of induction." We also saw how this problem will effect our lives. Let's assume for the moment that all occurrences of the Year 2000 problem are solved by the end of 1999. Will the problem go away.
Not necessarily. The real problem is that computer practitioners confuse the computer system's "interpretation" of a system predicate (__IS_CURRENT_DATE) with the actual predicate (__IS_CURRENT_DATE PRIOR TO T; UNDETERMINED THEREAFTER). Even if the Year 2000 problem disappears, we will still have to deal with the "elapsed time in Unix" problem. A manual might say that Unix function x produces today's date in Register 1. In fact, it won't "report" the date at all, rather it will "calculate the date on the basis of the number of seconds which have expired since January 1, 1970, until count, t, reaches 2**31; and the number of seconds since January 18, 2038 thereafter until count, t, reaches ..., etc." Naively, we have designed our programs for the projectable predicates described in our manuals, and not for the non-projectable predicates which underlay them.
To make matters more complicated, there are several four-byte REPORT_DATE standards (ISO, Microsoft, European) in use which are all incompatible with one another. Will manuals of the future report that function x reports "current date," on the one hand, or "current date only if one is using version, b, of operating system, OSk, prior to time, t, in Microsoft format," on the other?
In retrospect, a viable solution to the Year 2000 problems (in general) was to have been found in Geochronology all along. The earth's geologic time clock started roughly 4 billion years ago. Assuming that we are not yet at the mid-point of the earth's evolution we need to keep track of less than 10**18 seconds or 3x10**11, years which, for all practical purposes, can fit within a 64-bits. So, were systems designers and architects inspired by geochronologists they would have selected a 64-bit date field to begin with. Even this might be excessive. The dinosaurs, for example, only lived for 200 million years and they demonstrated far less propensity for self-destruction than humans. If we don't out-live them, we could save 4 bits! In any case, according to Jones' estimates, if the use of this double-word, expanded date field gobbled up $200 billion dollars over the last 50 years, we would have still come out ahead by the year 2000.
But the more interesting issue is whether are there other Year 2000-type problems of which we are unaware? How many more "new riddles" are there? The "year 2000" problem, Unix's "elapsed time since 1/1/1970" problem and others of this ilk are the residue of faulty introspection in our software engineering efforts. Perhaps detection models for predicate projectability and sundry other "new riddles" of inductive reasoning should be added to our working stock of software metrics. According to Jones, the "optimal time" to begin the Year 2000 repairs was 1995 or earlier, with October, 1997 as the last point that a mid-size corporation could commence their repairs with any hope of finishing by 2000. Perhaps the time to look for these detectable, though not-yet-detected, new riddles is now.